Посібник
"Геометрія трикутника" є методичним забезпеченням факультативних занять з математики в середніх навчальних закладах. Зміст матеріалу посібника відповідає програмі факультативних курсів з математики, що затверджені
Міністерством освіти України в 2017 році. Даний посібник призначений
для роботи в профільних класах природничо-математичного напрямку. У 2017/2018 навчальному році розпочато
апробацію підручника на факультативах в 7-8-9-х профільних класах міста Вінниці.
Метою публікації
даного методичного посібника
є ознайомлення педогогів міста з креативними технологіями у навчальному процесі, надання методичної допомоги вчителям математики, які
працюють або працюватимуть за інтерактивною
методикою, у технологічному
моделюванні навчально-інформаційного середовища, в організації самоконтролю і системного зовнішнього контролю за досягненнями учнів.
Автори посібника виходять з того, що геометрія, як
точна наука, допомагає людині системно сприймати навколишній світ. Розвиваюча
мета навчання за посібником
сприятиме формуванню цілісної гами уявлень про трикутник на площині, удосконалення навичок і умінь застосувати властивості
трикутників при розв'язуванні практичних завдань.
Значення креативних і особістисно-орієнтовних
підходів ще вагоміше, якщо враховувати профільну спрямованість сучасної старшої школи.
Автори врахували та зважили основні вимоги
користувачів навчальними посібниками.
Основними
користувачами даного методичного посібника стануть, у переважній більшості, вчителі математики. Проте цей посібник сформовано як підручник для учнів, які поглиблено вивчатимуть
математику. Тому в посібнику велику увагу приділено формуванню просторових та площинних
уявлень і навичок у процесі розв'язування творчих задач. В центрі уваги авторів посібника була системна реалізація виховних цілей, які здійснюється на засадах методології математичного моделювання. Зокрема, концепція розвиваючого та креативного
навчання передбачає оволодіння учнями способами розв’язання проблеми досліджень. Саме через
педагогічне моделювання навчальної проблеми
реалізується в посібнику системні дослідження властивостей трикутника, через формування уявлень про абстрактну модель (геометричну фігуру), це сприяє ґрунтовному засвоєнню опорних понять про неї, особливо,
під час вивчення
інваріантних властивостей у певному
контексті (зокрема, динамічному).
Реалізуючи завдання розвитку логічного мислення учнів, автори посібника не
зводили його до завдання формально-логічної побудови аксіоматичної теорії
геометрії трикутника (та її неможливо у повному обсязі реалізувати на рівні
середньої школи). Практична реалізація традиційних і нових педагогічних
технологій , їх використання при
масовому вивченні математики розглядаються у формах інтерактивного засвоєння учнями програмового
матеріалу. Проте , у більшості випадках (особливо на факультативних заняттях та гуртках), математична задача являється
засобом для доцільного розвитку логічного мислення, через обгрунтування
істини, як основної характеристики пізнавального процесу. Без сумніву, сучасна математична задача є
носієм великої навчальної інформації, а конкретніше навчальних функцій (навчання, виховання, розвитку, організації, контролю). На
думку авторів, відмова від розв’язування нестандартних задач на факультативах з математики або суто формальний підхід до їх розв’язання дуже небезпечно для процесу формування в
учнів творчих здібностей.
Для підвищення
ефективності розвиваючого навчання автор запропонував систематизовані серії
задач, які разом з дидактичними функціями спрямованні на формування в
учнів творчого мислення.
У посібнику підібрано такі задачі, в процесі розв’язання яких:
·
учням
мотивується доцільність вивчення нового
матеріалу, здоровий глузд геометричних визначень, корисність обґрунтування
властивостей трикутників;
·
учні
залучаються до самостійного відкриття того чи іншого геометричного факту, до
застосування обґрунтованих положень у
нових ситуаціях;
·
учні
послідовно підходять до самостійного
використання способів доведення теорем, до встановлення нових зв’язків між відомими їм геометричними поняттями;
·
в учнів формуються навички та уміння використовувати основні
методи наукового пізнання (досвід, дослід, спостереження, порівняння, аналогія,
аналіз, синтез, узагальнення, систематизація та
інтуїція);
·
учні
виявляють взаємозв’язок між алгеброю та геометрією.
·
учні
залучаються до самостійних пошукових досліджень за допомогою системного вивчення
розв’язків та отриманих результатів, зміни умови та узагальнення задач, пошук
різних способів та вибір серед них найоптимальнішого, який у повному обсязі задовольняє умовам поставленої задачі;
·
в учнів
формується якісна інтелектуальна сфера
розвитку мислення (активність, гнучкість,
глибина, критичність, доказовість та
ін.) .
У нашому посібнику
методично у повному обсязі розроблені заняття з розширеним теоретичними та
дидактичним матеріалом. Дидактичний
матеріал розподілено на секції за рівнями. За власним бажанням вчитель
може добирати з різних секцій і
формувати свій банк диференційованих задач, у відповідності до поставлених
цілей. Автори посібника щиро бажають успіхів усім користувачам посібника і вдячні усім, хто не тільки
використовуватиме наші методичні рекомендації, а й поділиться власним досвідом у роботі над
подібними розробками. Відгуки на
цей посібник просимо надсилати.
Медіани трикутника
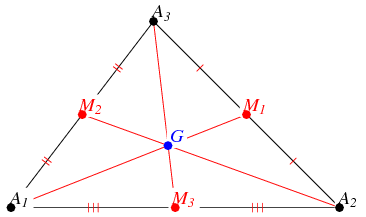
Медіана 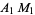 трикутника
трикутника 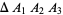 являється Cevian, що виходе із однієї вершини
являється Cevian, що виходе із однієї вершини 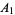 до середи в точке
до середи в точке 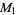 протилежної сторони. Три медіани будь-якого трикутника перетинаються одночасно (Casey 1888, стр. 3), в середині трикутника центроїда (Дурелл 1928)
протилежної сторони. Три медіани будь-якого трикутника перетинаються одночасно (Casey 1888, стр. 3), в середині трикутника центроїда (Дурелл 1928) 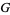 , яка має має координати трилінійні
, яка має має координати трилінійні 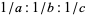 . Крім того, медіани трикутника ділять одна одну у відношенні 2: 1 (Casey 1888, стр . 3). Медіана також ділить пополам площу трикутника.
. Крім того, медіани трикутника ділять одна одну у відношенні 2: 1 (Casey 1888, стр . 3). Медіана також ділить пополам площу трикутника.
Нехай 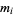 позначає довжину медіани із сторони
позначає довжину медіани із сторони 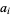 . тоді
. тоді
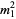 | 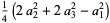 |
(1)
| |
(2)
|
(Casey 1888, стр 23;. Джонсон 1929, стр 68.).
(3)
|
де
(4)
|