„Творчість — це просто створення зв'язків між речами. Коли творчих людей питають, як вони щось зробили, вони відчувають себе трохи винуватими, тому що вони не зробили нічого насправді, а просто помітили. Це стає їм зрозуміло з часом. Вони змогли зв'язати різні шматочки свого досвіду і синтезувати щось нове. Це відбувається тому, що вони пережили й побачили більше, ніж інші, або тому, що вони більше про це думають“ Стів ДЖОБС.
Пояснювальна записка
Факультативний курс «Геометрія
куба» містить п’ять дидактичних
розділів:
1. ВСТУП. ЕЛЕМЕНТИ КУБА. (2 години)
2. ВЛАСТИВОСТІ КУБА. (9 години)
3. КУБ І
ПІРАМІДИ. (7 години)
4. КУБ І ТІЛА ОБЕРТАННЯ (14 години)
5.
УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ КУРСУ (2 години).
Кожний
розділ курсу має відповідну заохочувальну
траєкторію розвитку з практично-дослідницьким навчанням, що спирається на
триєдину мету. При цьому у курсі превалює
навчання між однолітками, що добре володіють навичками та
уміннями працювати з тілами. На заняттях прищеплюється самодисципліна заради
персональних цінностей і навчальних досягнень. Навчальна праця в даному курсі сприяє розвитку дослідницьких компетенцій
особистості старшокласника. Курс вчить
орієнтації у геометричному просторі тривимірних тіл. Он-лайнова практичність курсу, включаючи
зосередження на користувацьких уміннях, допомагає слухачам курсу оволодіти не тільки знаннями, а й геометричним
програмним забезпеченням. Кожний етап дослідницької діяльності в інформаційній
системі курсу поділено на події: розпізнавання проблеми, виявлення парадоксів або
непоміченої інформаційної реальності; опис
рівнів організації зв’язків,
групові залежності в просторових тілах, креативні
процеси конструювання тіл за заданими властивостями. Курс дає можливість
спільної чи одинарної обробки інформації про властивості просторових тіл.
Логічна інфраструктура вербального середовища курсу розвиває здібності та можливості
інтелектуального та практичного опанування методикою дослідження.
Для вирішення поставлених
завдань і досягнення мети, а саме навчанню досліджувати, в курсі застосовані
такі методи високого інтелектуального рівня: метод комплексного аналізу для
визначення: 1)куба, як геометричного об’єкта, 2)кількісні властивості куба, як предмета
вивчення, 3)динаміки при обертанні куба, як елементарного руху. Дидактичні цілі до завдань на дослідження
мають: 1) контекстні межі уявної області куба, як ідеального тіла, що
вивчається, і його структури; 2) елементів куба, компонованих об’єктів, явищ і процесів, що мають відношення до поставленої
мети; 3)розбиття наочної області на комплекси уявлень, що власне вивчається. Взагалі
в цьому курсі велику роль відіграє зовнішнє геометричне середовище для поняття «куб»
і його вишукані аналітичні методи теоретичного дослідження: 1)аналіз наукової
літератури; 2)Інтернет-ресурсів; 3)геометричних стандартів і геометричної історії;
4)вивчення і узагальнення практичного
досвіду. Системно-структурні методи: 1) аналізу; 2)зіставлення; 3)порівняння; 4)класифікації;
5)систематизація
з метою визначення стану досліджень у
обраній уявній області знань про куб.
Важливо для слухачів курсу проводити
аналогії, використовуючи методи
концептуально-порівняльного аналізу для виявлення понятійно-категоріального
апарату, визначення теоретичних і прикладних аспектів дослідження, визначення
структури і змісту неоднозначностей; аксіоматичний метод для осмислення тракутвань
«Діє у зв’язці з чим» і «Яка система оцінок ефективності дій об’єкта з точки зору
суб’єкта – людини». У курсі використано
діалектичні методи прагматичного рівня: методи теорії надійності систем
«людина-куб-середовище» для вибору переліку та структури показників
ефективності в архітектурі, якості та надійності кубічних конструкцій; методи ергономіки для
розробки житлових будівль..
Інформаційні мережеві
технології при постановці дослідів над
геометричним кубом проводять своєрідну ергономічну експертизу властивостей прямо
на очах у слухачів курсу. Зрозуміло, що методи
математичної статистики не достатні для розрахунку показників безпомилковості властивостей
куба і його найближчого середовища тіл.
Важливим для факультативного
курсу автор вважає методи емпіричного рівня: 1)спостереження за рухом та
динамікою змін елементів куба і реєстрація фактів зміни одних властивостей на
інші; 2)алгоритмічний аналіз програмування зміни координат вершин куба, за аналітичними
формулами; 3) статистика усіх наборів виконання дій, операцій і завдань над кубом,
своєрідне анкетування або тестування. Наведена
інформація дозволяє повніше сприйняти
викладені у курсі питання, яка може мати як самостійну цінність так і
корисність для слухачів.
Цей факультативний курс
створює потужне дослідницько-виховне середовище у середньому
закладі, в якому здібні старшокласники
мають можливість реалізувати свій
потенціал у конкуруючому середовищі з
метою оптимальної та успішної практики самореалізації. Інформаційне моделювання
властивостей куба дає можливість запобігти диссинхронізації розвитку особи, що діагностує випереджаючий розвиток інтелектуальної сфери в
порівнянні з психо-емоційною сферою або
практичною сферою застосувань умінь та навичок. Пошукова колективна робота та
дослідницька співпраця учнів у різних уявних просторах і мікрокліматах об’єктів сприяє інтелектуальній та
психо-емоційній напрузі. У свою чергу це збагачує практичний досвід старшокласників.
База навчання
геометрії куба – це Інтернет, мережа надає інформаційні ресурси для збагачення кругозору
і досвіду слухачів. Класична лекція чи урок не замінить неповнолітньому
емоційного занурення в оточені вчених та фахівців в процес здійснення і
відкриття невідомої реальності. І, незважаючи на те, що проведено величезну
кількість досліджень в області геометрії куба, проте все-таки для удосконалення
підліткової уяви просторів, способу
дослідження куба, маємо організувати співпрацю обдарованих дітей. Це відповідає запитам підкріплення думки
персональним досвідом уявлення. Практика факультативного навчання старшокласника реалізується через ланцюгові «успіхи» та поступові перемоги над
самим собою. Отриманий досвід
усвідомленої навчальної співпраці старшокласників
з інформаційними моделями про властивості куба, електронними доробками фахівців
з відповідних напрямів спеціалізації дає позитивний результат. Автор факультативу розуміє, що досить глибоко
занурювати старшокласників в непрості проблемні наукові питання зараз не варто. Проте варто
показати те, як невидиме, приховане або
лише уявлюване трансформується у виявлене і зафіксоване. Такі початкові
індикатори уяви запропонують згодом
слухачам парадокси-проблеми і вони зреагують на особливі маячки і таким чином відкриють у собі джерела і унікальні детермінанти
творчості.
Курс має допомогти слухачам налагодити взаємозв'язки
з творчими однолітками за кордоном. Саме
через співпрацю з компетентними фахівцями досягати у старшокласників глибокого
уявлення про поняття власного потенціалу особистості. Належно використовувати інтелектуальний ресурс
за умов творчої самореалізації в конкуруючому
мікрокліматі.
Проблема оптимальної реалізації здібностей слухачів мислити та уявляти стоїть перед курсом.
Як розвивати аспектні здібності в обдарованих неповнолітніх право наставника.
Проте актуалізація усієї структури
обдарованості, таланту і здібностей має дуже велике мотиваційне значення як для
професійного визначення, так і для вирішення конкретних психолого-емоційних спонукань
до дослідження невідомого.
Навчальна програма факультативного курсу
«Геометрія куба» складена для
старшокласників 9,10,11,12 спеціалізованих класів і має реалізувати напрямки
навчально-дослідницької діяльності:
·
допомогти
актуалізувати знання та мотивувати юнаків
та дівчат до творчої співпраці та надолужити відставання інформаційного
кругозору старшокласників, притлумити негативний відтінок натаскування та
зубріння.
·
розвивати
свої задатки та здібності через осмислення своїх прав та обов’язків у колі причин
та наслідків отриманого творчого досвіду
під час участі у конкурсах, змаганнях, випробуваннях, олімпіадах, фестивалях, форумах;
·
допомогти
старшокласникам оптимально визначати важливі пріоритети та базові орієнтири
щодо психологічного та соціального
саморозвитку, а саме персональних унікальних особливостей у конкуруючому
середовищі;
·
допомогти
соціально самоорганізуватися і самореалізувати себе на рівні власних можливостей, через внутрішні та зовнішні
чинники сприяти розвитку спеціальних здібностей старшокласників у конкуруючих середовищах,
підтримати емоційне відношення до дійсності.
На даний період дуже популярні методики
розвитку партнерства у підлітків, що навчаються у різних закладах. Варто
звернути увагу на те, що одні методики дійсно дають відмінний результат в дослідницькій
роботі, а деякі методики просто рекламуються у виданнях і не мають навіть
задовільного втілення! Даний факультативний курс дасть можливість виявити
загальні проблеми обдарованих дітей і зрозуміти, що може зробити сама дитина,
що може зробити для цієї дитини школа, а що – можуть батьки дитини. Наставник факультативного
курсу матиме радість від співпраці з старшокласниками, якщо допоможе і
сприятиме розкриттю персональних задатків, здібностей, і
дасть зрозуміти, що робота з різними інсинуаціями, міфами, стереотипами, псевдонауковими
поглядами завжди є ефективною і чудовою
для встановлення закономірної дійсності.
Поділюсь
з наставниками курсу власним досвідом. За потребою я застосовував диференційоване
опанування курсом, якщо між старшокласниками виникли дві групи по типу
"зроблений" вундеркінд та
"природній" талант. Якщо ж наставник здібний швидко рефлексувати
перед старшокласниками і розумітиме, що їм це потрібно, то у найкращому випадку
ця молодь має відповісти сама собі на запитання, як скоригувати цей курс, щоб він вплинув на їхнє
подальше життя? У підлітковому віці
особі варто навчитися самовизначатися і закріпляти надважливу
здібність обдарованих осіб – це приймати рішення самостійно. Здебільшого в наш
кризовий час наставники частіше зустрічаються з так званим феноменом згасання
ранньої обдарованості у підлітковому віці. Не
варто фарбувати явища обдарованості в райдужні барви. Як правило, у
обдарованих неповнолітніх не було
веселкового дитинства. Їхнє теперішнє вже загублене в минулому. А тому цей
факультативний курс має провести відповідну корекцію мислення у задоволенні
потреб згасаючої обдарованості особи заради його успішного майбутнього.
У
обдарованих підлітків є проблема «прив’язаності» до взірцевого об’єкта, з яким
він ділиться своїми таємними та ймовірними очікуваннями. Тому наставнику курсу
варто урізноманітнити точки зору даної
особи на дослідницьку проблему через спілкування та дослідницькою роботою з фахівцями різних напрямів.
У
підлітковому віці обдарованим вчитися стає досить важко. Настає так звана
примарна перша «границя освіти» або перша «межа розвитку» особистості. І це вже
справа сумлінності наставника курсу, як підвести молодь до того, щоб вони заперечили
цей примарний міф, який існує до тих пір, поки йому не знаходиться внутрішнє
заперечення особистості. Тоді процес дослідницького навчання стає привабливим і
приємним. Дорослі, які не вислуховують дітей чи підлітків, – мають приховану «бездарність», просто здогадуються, що інтуїтивно діти
заперечують тільки те, що їм не зрозуміле, не притаманне, не властиве, чого
вони ще бояться і неспроможні виконувати практично. Я би порадив наставникам
робити висновки на користь того, що запропонували старшокласники, інтуїтивно в запереченні
вони знаходять свій шлях у «проблемі» самостійно, і виправляють помилки і вчаться
самотужки. Наставнику курсу треба часто проводити аналіз творчих проблем, їх діагностику, прогнозування промахів, тобто супроводу
обдарованості.
Календарно-тематичне
планування
факультативного
курсу «Геометрія куба»
10-11 КЛАС (35 годин на рік)
(1 ГОД НА ТИЖДЕНЬ - 1 СЕМЕСТР (16 тижнів 16 годин),
1 ГОД НА ТИЖДЕНЬ - 2 СЕМЕСТР(19 тижнів
19 годин))
№
|
ТЕМА ЗАНЯТТЯ
, ВИДИ ПИСЬМОВИХ РОБІТ УЧНІВ
|
годин
|
дата
|
1.ВСТУП. ЕЛЕМЕНТИ КУБА.
|
2
|
||
1
|
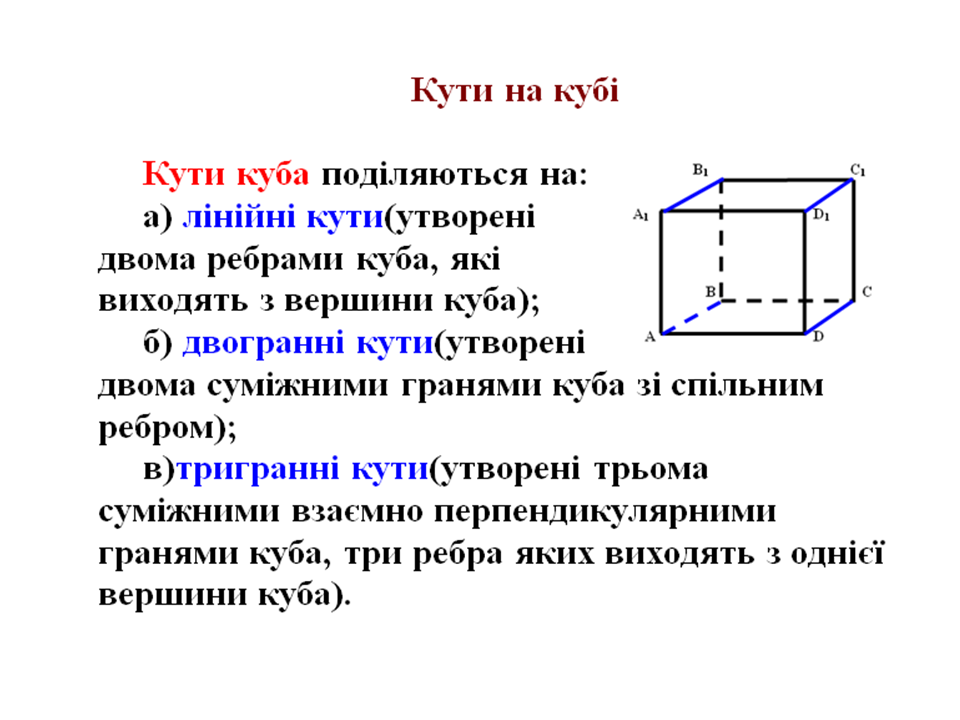
ВСТУП. Поняття многогранного кута у просторі.
Лінійні кути(плоскі кути) на кубі. Двогранний кут на кубі. Тригранний кут на
кубі. Властивості многогранних кутів у кубі. Розв’язування задач на двогранних кутах куба.
|
1
|
09.09
|
2
|
Існування випуклих і невипуклих многогранників.
Призми. Класифікація елементів призм.
Нуль-мірні, одномірні, двомірні, тривимірні елементи призми. Історичний
розвиток зображень призм на площині. Поняття ортогональної та паралельної
проекції призми на площину. Ілюстрація різних видів розгорток 3-кутної та 4-кутної призми. Різні види
розгорток куба.
|
1
|
16.09
|
2.ВЛАСТИВОСТІ КУБА
|
9
|
||
3
|
Прямі і похилі паралелепіпеди. Куб. Властивості
розфарбування вершин та граней паралелепіпедів у різні кольори. Властивості
діагоналей паралелепіпедів.
|
1
|
23.09
|
4
|
Відновлення призми за її розгорткою. Одинадцять
різних класичних розгорток куба. Теореми Коші і Александрова про випуклий
многогранник. Існування випуклого і не випуклого многогранника з рівними
граннями і різними об’ємами.
|
30.09
|
|
5
|
Ромбоїди. Властивості діагоналей ромбоїда. Основні властивості
лінійних елементів прямокутних паралелепіпедів. Комбінаторні властивості
двомірних елементів паралелепіпеда.
Властивості розфарбування ребер паралелепіпедів
у різні кольори.
|
1
|
06.10
|
6
|
Основні властивості відстаней між двовимірними
елементами прямокутних паралелепіпедів. Комбінаторні властивості взаємних
розташувань граней паралелепіпедів. Властивості розфарбування граней
паралелепіпедів у різні кольори. Існування тридцяти різних розфарбувань
кубика-рубика.
|
1
|
13. 10
|
7
|
Властивості кутів між лінійними елементами
прямокутних паралелепіпедів та куба. Побудова перерізу куба січною площиною
способом слідів. Властивості розфарбування граней паралелепіпедів у різні
кольори.
|
1
|
20. 10
|
8
|
Властивості кутів і відстаней між двовимірними
елементами куба. Многокутник, як
переріз куба площиною. Існування трьох видів правильного перерізу куба
площиною. Умови можливості розрізання куба
на рівні тривимірні елементи(рівні призми і прямокутні піраміди).
|
1
|
27. 10
|
9
|
Рівняння куба в просторовій системі координат.
Задачі на екстремальні значення на кубі.
Екстремальні значення лінійних функцій, що задані на кубі. Теорема Канторовича про екстремум
лінійної функції на межі многогранника.
|
1
|
06.11
|
11
|
Куля і сфера, що вписані в куб. Симетрія куба та симетрія перерізу куба
січною площиною.
Використання куба в практичній діяльності.
Тримірні частини куба. Клин. Призматоїд. Головоломки Ешера з неможливими кубами. Кубічний годинник.
|
1
|
13. 11
|
3.КУБ І ПІРАМІДИ.
|
7
|
||
12
|
Піраміди. Класифікація елементів піраміди. Класифікація пірамід за їх
розгортками. Правильні піраміди. Властивості взаємного розміщення ребер,
висот, апофем, граней правильного тетраедра. Існування та властивості двох
правильних тетраедрів з вершинами на кубі. Кількість класичних розгорток
правильного тетраедра.
|
1
|
20. 11
|
13
|
Піраміди, в яких бічні ребра нахилені до площини
основи під рівними кутами. Властивості двох різних чотирикутних пірамід з
вершинами на кубі. Властивості
взаємного розміщення.
|
1
|
03. 12
|
14
|
Піраміди, в яких усі двогранні кути при основі
рівні між собою.
Існування п’яти різних пірамід у кубі, з
вершинами на кубі.
|
1
|
10. 12
|
15
|
Піраміди, в яких усі дві суміжні бічні грані
перпендикулярні до площини основи. Комбінаторні властивості розташування
різних видів трикутних пірамід на вершинах паралелепіпеда. Вписаний куб в
правильну чотирикутну піраміду. Властивості взаємного розміщення.
|
1
|
17.12
|
16
|
Піраміди, в яких одна бічна грань перпендикулярна до площини основи. Описана
і вписана піраміда та її властивості.
|
1
|
20.12
|
17
|
Зрізані чотирикутні піраміди та їх властивості. Вписаний
куб у зрізану чотирикутну піраміду. Властивості взаємного розміщення. Використання
їх на практиці.
|
1
|
25.12
|
18
|
Правильні тіла. Вписані правильні тіла в куб.
Описані правильні тіла навколо куба. Перпендикулярність правильного перерізу
куба до діагоналі куба.
|
1
|
13.01
|
4.КУБ І ТІЛА ОБЕРТАННЯ
|
14
|
||
19
|
Тіла обертання. Прямі циліндри. Елементи
циліндра. Переріз циліндра січною площиною. Куб, що вписаний в циліндр. Куб,
що описаний навколо циліндра. Властивості взаємного розміщення. Використання
їх на практиці.
|
1
|
20.01
|
20
|
Прямі конуси та їх властивості конічних перерізів.
Куб і конус. Властивості взаємного розміщення. Використання їх на практиці.
|
1
|
27.01
|
21
|
Зрізані конуси та їх властивості конічних
перерізів. Куб і зрізаний конус. Властивості взаємного розміщення.
Використання їх на практиці.
|
1
|
4.02
|
22
|
Кулі, сфери та їх властивості конічних
перерізів. Куб і куля. Властивості взаємного розміщення. Використання їх на
практиці.
|
1
|
11.02
|
23
|
Кульові сектори та сегменти. Кулі, сфери та їх
властивості січних і дотичних площин. Куб, що вписаний в кульовий сегмент.
Властивості взаємного розміщення. Використання їх на практиці.
|
1
|
18.02
|
24
|
Комбінації геометричних тіл з
кубом. Октаедр і куб. Властивості взаємного розміщення. Використання їх на
практиці.
|
1
|
25.02
|
25
|
Циліндри, описані навколо куба і вписані в куб.
Властивості взаємного розміщення. Використання їх на практиці.
|
1
|
4.03
|
26
|
Конуси, описані навколо
піраміди і вписані в піраміду. Властивості взаємного розміщення.
Використання їх на практиці.
|
1
|
11.03
|
27
|
Кулі та сфери, описані навколо
призми.
|
1
|
17.03
|
28
|
Кулі та сфери, описані навколо
піраміди або конуса.
|
1
|
2.04
|
29
|
Кулі, вписані в піраміду або в
конус.
|
1
|
9.04
|
30
|
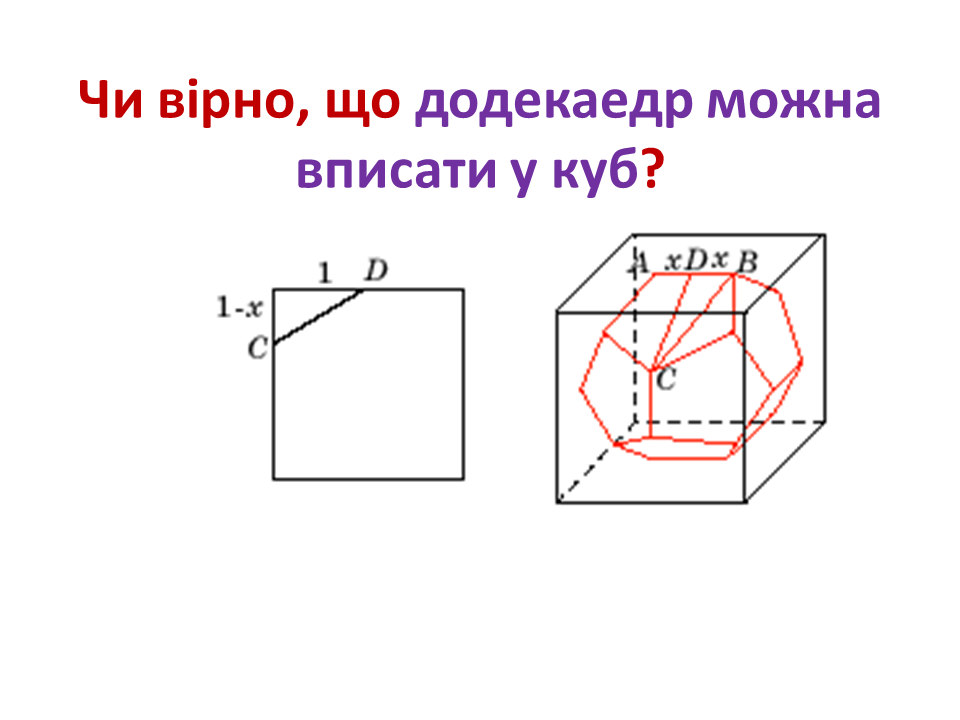
Комбінації кулі, додекаедра і куба.
|
1
|
16.04
|
31
|
Тіла, утворені обертанням кубів, навколо осі
симетрії, навколо довільних прямих, що перетинають куб.
|
1
|
23.04
|
32
|
Побудова
методом слідів перерізу піраміди січною площиною. Обчислення площі перерізу
піраміди. Існування правильного
перерізу правильного тетраедра, що паралельний двом несуміжним ребрам
правильного тетраедра.
|
1
|
30.04
|
33
|
Побудова
методом внутрішніх проекцій перерізу куба площиною. Обчислення площі перерізу
куба. Трикутник, чотирикутник, п’ятикутник та шестикутник в перерізі площиною
куба. Неможливість отримання правильного п’ятикутника в перерізі куба
площиною.
|
1
|
03.05
|
5.УЗАГАЛЬНЕННЯ ТА
СИСТЕМАТИЗАЦІЯ КУРСУ
|
2
|
||
34
|
Властивості тетраедра, що
побудований на діагоналях бічних граней куба. Симетрія геометричних тіл. Усі
види симетрії правильних тіл.
Усі види симетрії
правильного тетраедра, куба. Захист науково-дослідних робіт.
|
1
|
14.05
|
35
|
Комбінаторні задачі на розфарбування граней
геометричних тіл. Захист науково-дослідних робіт.
Заповнення простору правильними тілами і шахове
розфарбування простору..
|
1
|
23.05
|
Зміст програми
факультативного
курсу «Геометрія куба»
№
п/п
|
Зміст навчального матеріалу
|
Основні вимоги
до підготовки учнів
|
Усього годин
|
В тому числі
|
|
Теоретичні
роботи
|
Практичні
роботи
|
||||
1.ВСТУП. ЕЛЕМЕНТИ КУБА.
Поняття многогранного кута у просторі. Лінійні
кути(плоскі кути) на кубі. Двогранний кут на кубі. Тригранний кут на кубі.
Властивості многогранних кутів у кубі. Розв’язування задач на двогранних кутах куба.
Існування випуклих і невипуклих многогранників.
Призми. Класифікація елементів призм.
Нуль-мірні, одномірні, двомірні, тривимірні елементи призми. Історичний
розвиток зображень призм на площині. Поняття ортогональної та паралельної
проекції призми на площину. Ілюстрація різних видів розгорток 3-кутної та 4-кутної призми. Різні види
розгорток куба.
|
Учні повинні:
мати уявлення про об’єкт вивчення геометричних властивостей куба;
виявляти зв’язок куба з призмами;
усвідомити практичне значення куба для сучасної людини;
знати
визначення куба як геометричного
тіла з трьома вимірами.
називати предмет вивчення геометрії куба;
пояснювати зв'язок геометрії куба з практичними застосуваннями;
усвідомлювати практичне значення властивостей куба;
уміти
знаходити
інформацію про поняття:
·
куб;
·
розгортка
куба;
·
використання
куба.
|
2
|
2
|
2
|
|
2.ВЛАСТИВОСТІ КУБА
|
9
|
9
|
7
|
||
ВЛАСТИВОСТІ КУБА(9 годин)
Прямі і похилі паралелепіпеди. Куб. Властивості
розфарбування вершин та граней паралелепіпедів у різні кольори. Властивості
діагоналей паралелепіпедів.
Відновлення призми за її розгорткою. Одинадцять
різних класичних розгорток куба.
Теореми Коші і Александрова про випуклий
многогранник. Існування випуклого і не випуклого многогранника з рівними
граннями і різними об’ємами.
Ромбоїди. Властивості діагоналей ромбоїда. Основні властивості
лінійних елементів прямокутних паралелепіпедів. Комбінаторні властивості
двомірних елементів паралелепіпеда.
Властивості розфарбування ребер паралелепіпедів
у різні кольори.
Основні властивості відстаней між двовимірними
елементами прямокутних паралелепіпедів. Комбінаторні властивості взаємних
розташувань граней паралелепіпедів. Властивості розфарбування граней
паралелепіпедів у різні кольори. Існування тридцяти різних розфарбувань
кубика-рубика.
Властивості кутів між лінійними елементами
прямокутних паралелепіпедів та куба. Побудова перерізу куба січною площиною
способом слідів. Властивості розфарбування граней паралелепіпедів у різні
кольори.
Властивості кутів і відстаней між двовимірними
елементами куба. Многокутник, як
переріз куба площиною. Існування трьох видів правильного перерізу куба
площиною. Умови можливості розрізання куба
на рівні тривимірні елементи(рівні призми і прямокутні піраміди).
Рівняння куба в просторовій системі координат.
Задачі на екстремальні значення на кубі.
Екстремальні значення лінійних функцій, що задані на кубі. Теорема Канторовича про екстремум
лінійної функції на межі многогранника.
Куля і сфера, що вписані в куб. Симетрія куба та симетрія перерізу уба
січною площиною.
Використання куба в практичній діяльності.
Тримірні частини куба. Клин. Призматоїд. Головоломки Ешера з неможливими кубами. Кубічний годинник.
3.КУБ І ПІРАМІДИ. (7 ГОД)
Піраміди. Класифікація елементів піраміди. Класифікація пірамід за їх
розгортками. Правильні піраміди. Властивості взаємного розміщення ребер,
висот, апофем, граней правильного тетраедра. Існування та властивості двох
правильних тетраедрів з вершинами на кубі. Кількість класичних розгорток
правильного тетраедра.
Піраміди, в яких бічні ребра нахилені до площини
основи під рівними кутами. Властивості двох різних чотирикутних пірамід з
вершинами на кубі. Властивості
взаємного розміщення.
Піраміди, в яких усі двогранні кути при основі
рівні між собою.
Існування п’яти різних пірамід у кубі, з
вершинами на кубі.
Піраміди, в яких усі дві суміжні бічні грані
перпендикулярні до площини основи. Комбінаторні властивості розташування
різних видів трикутних пірамід на вершинах паралелепіпеда. Вписаний куб в
правильну чотирикутну піраміду. Властивості взаємного розміщення.
Піраміди, в яких одна бічна грань перпендикулярна до площини основи. Описана
і вписана піраміда та її властивості.
Зрізані чотирикутні піраміди та їх властивості. Вписаний
куб у зрізану чотирикутну піраміду. Властивості взаємного розміщення. Використання
їх на практиці.
Правильні тіла. Вписані правильні тіла в куб.
Описані правильні тіла навколо куба. Перпендикулярність правильного перерізу
куба до діагоналі куба.
|
Учні повинні:
мати
уявлення про властивості вершин куба,
властивості ребер куба,
властивості діагоналей куба, властивості діагоналей граней куба
властивості граней куба,
властивості розгорток
куба, теореми Коші, теореми Александрова, ромбоїди та паралелепіпеди та їх властивості,
властивості функцій, що задані на паралелепіпедах, характер розфабувань куба,
способи вивчення дослідження перерізів куба, моделювання перерізів куба,
відтворення куба на папері та в графіченому редакторі, використання
властивостей куба при розв’язування задач,
перетворення інформації про куб на практиці;
виявляти
і пояснювати зв’язок між термінами, властивостями, явищами, моделями, системними властивостями, функціями на кубі;
усвідомити практичне значення властивостей
для кодування інформації;
знати
систему дослідження
властивостей куба.
уміти
знаходити
інформацію про поняття:
· моделювання перерізів куба площиною;
· інформаційну модель куба як замкненого графа;
·
екстремальні
значення лінійних функцій на кубі;
·
властивість розташування кулі та куба.
Учні повинні:
мати уявлення про об’єкт вивчення геометричних властивостей піраміди;
виявляти зв’язок куба з пірамідами;
усвідомити практичне значення куба
і піраміди для науки і виробництва;
знати
визначення піраміди як геометричного тіла з трьома вимірами.
називати властивості
піраміди та куба;
пояснювати зв'язок геометрії куба та
піраміди з практичними застосуваннями;
усвідомлювати практичне значення властивостей пірамід у кубі;
уміти
знаходити
інформацію про поняття:
·
куб і
піраміду;
·
розгортка
піраміди;
·
використання
пірамід.
|
||||
4.КУБ І ТІЛА ОБЕРТАННЯ
|
14
|
14
|
12
|
||
Тіла обертання. Прямі циліндри. Елементи
циліндра. Переріз циліндра січною площиною. Куб, що вписаний в циліндр. Куб,
що описаний навколо циліндра. Властивості взаємного розміщення. Використання
їх на практиці.
Прямі конуси та їх властивості конічних перерізів.
Куб і конус. Властивості взаємного розміщення. Використання їх на практиці.
Зрізані конуси та їх властивості конічних
перерізів. Куб і зрізаний конус. Властивості взаємного розміщення.
Використання їх на практиці.
Кулі, сфери та їх властивості конічних
перерізів. Куб і куля. Властивості взаємного розміщення. Використання їх на
практиці.
Кульові сектори та сегменти. Кулі, сфери та їх
властивості січних і дотичних площин. Куб, що вписаний в кульовий сегмент.
Властивості взаємного розміщення. Використання їх на практиці.
Комбінації геометричних тіл з
кубом. Октаедр і куб. Властивості взаємного розміщення. Використання їх на
практиці.
Циліндри, описані навколо куба і вписані в куб.
Властивості взаємного розміщення. Використання їх на практиці.
Конуси, описані навколо
піраміди і вписані в піраміду. Властивості взаємного розміщення.
Використання їх на практиці.
Кулі та сфери, описані навколо
призми.
Кулі та сфери, описані навколо
піраміди або конуса.
Кулі, вписані в піраміду або в
конус.
Комбінації кулі, додекаедра і куба.
Тіла, утворені обертанням кубів, навколо осі
симетрії, навколо довільних прямих, що перетинають куб.
Побудова
методом слідів перерізу піраміди січною площиною. Обчислення площі перерізу
піраміди. Існування правильного
перерізу правильного тетраедра, що паралельний двом несуміжним ребрам
правильного тетраедра.
|
Учні повинні:
мати уявлення про об’єкт вивчення геометричних властивостей тіл обертання;
виявляти зв’язок куба з тілами обертання;
усвідомити практичне значення тіл
обертання для сучасної людини;
знати
визначення тіл обертання як геометричного тіла з трьома вимірами.
називати предмет вивчення геометрії тіл обертання;
пояснювати зв'язок геометрії куба з тілами обертання з практичними застосуваннями;
усвідомлювати практичне значення властивостей куба;
уміти
знаходити
інформацію про поняття:
·
кулю і
правильні тіла;
·
розгортки
сфери;
·
використання
кулі.
|
||||
Побудова
методом внутрішніх проекцій перерізу куба площиною. Обчислення площі перерізу
куба. Трикутник, чотирикутник, п’ятикутник та шестикутник в перерізі площиною
куба. Неможливість отримання правильного п’ятикутника в перерізі куба
площиною.
|
|||||
5.УЗАГАЛЬНЕННЯ ТА
СИСТЕМАТИЗАЦІЯ КУРСУ
|
|||||
Властивості тетраедра, що
побудований на діагоналях бічних граней куба. Симетрія геометричних тіл. Усі
види симетрії правильних тіл.
Усі види симетрії
правильного тетраедра, куба. Захист науково-дослідних робіт.
Комбінаторні задачі на розфарбування граней
геометричних тіл. Захист науково-дослідних робіт.
Заповнення простору правильними тілами і шахове
розфарбування простору..
|
Учні повинні:
мати уявлення про об’єкт вивчення геометричних властивостей правильних тіл та фігур;
виявляти зв’язок куба з правильними тілами;
усвідомити практичне значення правильних
тіл для сучасної людини;
знати
визначення правильних тіл як тіла з трьома вимірами.
називати предмет вивчення геометрії правильних тіл;
пояснювати зв'язок геометрії правильних тіл з практичними застосуваннями в
дослідженнях;
усвідомлювати практичне значення властивостей правильних тіл;
уміти
знаходити
інформацію про поняття:
·
правильні
тіла;
·
розгортку
правильних тіл;
·
використання
властивостей правильних тіл на практиці.
|
2
|
2
|
2
|
|






















































































































Немає коментарів:
Дописати коментар