Наприклад: Існує обмежена кількість ланцюгів простих чисел в деяких арифметичних прогресіях:
Наприклад, 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 є 10-терміновою арифметичною прогресією простих чисел з різницею 210.
Відносно прості числа
Наприклад, 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 є 10-терміновою арифметичною прогресією простих чисел з різницею 210.
Давно доведено, що існують довільно довгі послідовності простих чисел в арифметичній прогресії (Guy 1994). Ще в 1770 році Лагранж і Варинг досліджували, наскільки велика загальна різниця арифметичної прогресії 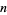 простих чисел. У 1923 році Харді та Літлвуд (1923) зробили дуже загальну гіпотезу, відому як гіпотеза k- tuple про розподіл первинних сузір'їв, що включає в себе гіпотезу, що існує нескінченно довгий простий арифметичний прогрес, як особливий випадок. Згодом важливий додатковий теоретичний прогрес зробив ван дер Кортут (1939), який довів, що в арифметичній прогресії існує нескінченно багато трійок простих чисел, а Хіт-Браун (1981), які довели, що існує нескінченно багато чотирирічного прогресії, що складаються з три прості числа і число, яке є або первинним, або напівпринципом .
простих чисел. У 1923 році Харді та Літлвуд (1923) зробили дуже загальну гіпотезу, відому як гіпотеза k- tuple про розподіл первинних сузір'їв, що включає в себе гіпотезу, що існує нескінченно довгий простий арифметичний прогрес, як особливий випадок. Згодом важливий додатковий теоретичний прогрес зробив ван дер Кортут (1939), який довів, що в арифметичній прогресії існує нескінченно багато трійок простих чисел, а Хіт-Браун (1981), які довели, що існує нескінченно багато чотирирічного прогресії, що складаються з три прості числа і число, яке є або первинним, або напівпринципом .
Проте, незважаючи на всі ці роботи, доказ загального результату для довільно довгих послідовностей простих чисел залишається відкритою гіпотезою (Гай 1994, стор. 15). Завдяки новій роботі Бена Гріна та Теренса Тао, здається, що припущення остаточно вирішено в позитивному. У нещодавно опублікованій препринті Грін та Тао (2004) використовують важливий результат, відомий як теорема Семереді в поєднанні з недавніми роботами Гольдстона та Йілдіріма, розумним "принципом переносу" та 48 сторінками щільної та технічної математики, що, очевидно, встановлюють основна теорема про те, що простими числами містяться арифметичні прогресії довжини 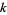 для всіх
для всіх 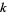 (Weisstein 2004). Однак доказ неконструктивний .
(Weisstein 2004). Однак доказ неконструктивний .
Розклад натурального числа, більшого ніж n= m((10^10)^10m) на суму п’яти доданків,
які є взаємно простими числами.
Гіпотеза: Нехай a, b, c,d, e являються натуральними числами, тоді парні
числа, більшого ніж n= m((10^10)^10m), можна подати, як суму п’яти доданків, які є взаємно простими числами: 2k= 2a +3b +5c +7d + 11е
Гіпотеза: Нехай a, b, c,d, e являються натуральними числами, тоді непарні
числа, більшого ніж n= m((10^10)^10m), можна подати, як суму п’яти доданків, які є взаємно простими числами: 2k+1= 3a +5b +7c +11d + 13е
Відносно прості числа
Означення. Два цілих числа відносно прості (або coprime ),
якщо немає цілого числа більше, ніж того, яке розділяє їх обох (тобто
їх найбільший загальний дільник є
одним). Наприклад, 12 і 13 відносно прості, але 12 і 14 не є.
Означення. цілих чисел є (взаємно) відносно простим,
якщо немає цілого числа, яке розділяє їх усіх. Наприклад, цілі числа 30,
42, 70 і 105 є взаємно відносними простими (але не попарно відносно простими ).
Це визначення узагальнено на багато інших розділів
математики. Наприклад, два поліноми з цілими коефіцієнтами є відносно
простими, якщо немає незвідного полінома, який розділяє їх обох.
Чи є в більшості арифметичних прогресі нескінченно багато простих ? Звичайно, не, якщо загальна відмінність має головний чинник, що є спільним з одним із умов (наприклад: 6, 9, 12, 15, ...). У 1837 році Діріхле довів, що у всіх інших випадках відповідь була так:
Нагадаємо, що теорема про простої кількості говорить, що для будь-якого заданого n існують асимптотичні n / log n простих чисел менше, ніж n . Аналогічно можна довести, що послідовність a + k * b ( k = 1,2,3, ...) містить асимптотичні n / ( phi ( b ) log n ) прості числа менше, ніж n . Ця оцінка не залежить від вибору a !
- Теорема Дирихле про початковість в арифметичних прогресії
- Якщо a та b є відносно простими натуральними числами, то арифметична прогресія a , a+ b , a +2 b , a +3 b , ... містить нескінченну кількість простих чисел.
Теорема Дірихле не говорить, що в цій послідовності є безліч послідовних значень, які є простими значеннями (це те, що ми хотіли б). Але гіпотеза Діксона вказує на те, що враховуючи будь-яке натуральне число n , то для кожної "прийнятної" арифметичної прогресії є n послідовних термінів, які є основними. У 1939 році ван дер Кортут показав, що у арифметичній прогресії існує нескінченно багато трійок простих [ Corput1939 ]. У 2004 році Грін і Дао [ GT2004a ] показали, що існують довільно довільні послідовності простих чисел і що до [ GT2004b ] відбувається k-термова послідовність простих чисел :
2 2 2 2 2 2 2 2 100 kОчевидно, це не оптимально! Він висловив припущення , що на насправді відбувається до до ! +1.
Також можна поставити це в кількісну форму і оцінити, скільки їх повинно бути, за евристикою . Наприклад, Гросвальд [ GH79 ] запропонував, що якщо N k - це число арифметичних прогресій k простих чисел менше, ніж N , то
де
Він зміг довести це для випадку k = 3 [GH79]. Зелений та Дао нещодавно довели це для k = 4 [ GT2006a ].
На наших сторінках евристики ми також даємо асимптотичні оцінки для числа з фіксованою довжиною k і фіксованою різницею d . Перша таблиця показує найбільші відомі прості числа в арифметичній послідовності (але лише третій термін і далі для кожної послідовності).
[ Переглянути всі прості у списку.]
2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113
127 131 137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223 227 229
233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349
353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463
467 479 487 491 499 503 509 521 523 541
547 557 563 569 571 577 587 593 599 601
607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733
739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863
877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997 1009 1013
1019 1021 1031 1033 1039 1049 1051 1061 1063 1069
1087 1091 1093 1097 1103 1109 1117 1123 1129 1151
1153 1163 1171 1181 1187 1193 1201 1213 1217 1223
1229 1231 1237 1249 1259 1277 1279 1283 1289 1291
1297 1301 1303 1307 1319 1321 1327 1361 1367 1373
1381 1399 1409 1423 1427 1429 1433 1439 1447 1451
1453 1459 1471 1481 1483 1487 1489 1493 1499 1511
1523 1531 1543 1549 1553 1559 1567 1571 1579 1583
1597 1601 1607 1609 1613 1619 1621 1627 1637 1657
1663 1667 1669 1693 1697 1699 1709 1721 1723 1733
1741 1747 1753 1759 1777 1783 1787 1789 1801 1811
1823 1831 1847 1861 1867 1871 1873 1877 1879 1889
1901 1907 1913 1931 1933 1949 1951 1973 1979 1987
1993 1997 1999 2003 2011 2017 2027 2029 2039 2053
2063 2069 2081 2083 2087 2089 2099 2111 2113 2129
2131 2137 2141 2143 2153 2161 2179 2203 2207 2213
2221 2237 2239 2243 2251 2267 2269 2273 2281 2287
2293 2297 2309 2311 2333 2339 2341 2347 2351 2357
2371 2377 2381 2383 2389 2393 2399 2411 2417 2423
2437 2441 2447 2459 2467 2473 2477 2503 2521 2531
2539 2543 2549 2551 2557 2579 2591 2593 2609 2617
2621 2633 2647 2657 2659 2663 2671 2677 2683 2687
2689 2693 2699 2707 2711 2713 2719 2729 2731 2741
2749 2753 2767 2777 2789 2791 2797 2801 2803 2819
2833 2837 2843 2851 2857 2861 2879 2887 2897 2903
2909 2917 2927 2939 2953 2957 2963 2969 2971 2999
3001 3011 3019 3023 3037 3041 3049 3061 3067 3079
3083 3089 3109 3119 3121 3137 3163 3167 3169 3181
3187 3191 3203 3209 3217 3221 3229 3251 3253 3257
3259 3271 3299 3301 3307 3313 3319 3323 3329 3331
3343 3347 3359 3361 3371 3373 3389 3391 3407 3413
3433 3449 3457 3461 3463 3467 3469 3491 3499 3511
3517 3527 3529 3533 3539 3541 3547 3557 3559 3571
3581 3583 3593 3607 3613 3617 3623 3631 3637 3643
3659 3671 3673 3677 3691 3697 3701 3709 3719 3727
3733 3739 3761 3767 3769 3779 3793 3797 3803 3821
3823 3833 3847 3851 3853 3863 3877 3881 3889 3907
3911 3917 3919 3923 3929 3931 3943 3947 3967 3989
4001 4003 4007 4013 4019 4021 4027 4049 4051 4057
4073 4079 4091 4093 4099 4111 4127 4129 4133 4139
4153 4157 4159 4177 4201 4211 4217 4219 4229 4231
4241 4243 4253 4259 4261 4271 4273 4283 4289 4297
4327 4337 4339 4349 4357 4363 4373 4391 4397 4409
4421 4423 4441 4447 4451 4457 4463 4481 4483 4493
4507 4513 4517 4519 4523 4547 4549 4561 4567 4583
4591 4597 4603 4621 4637 4639 4643 4649 4651 4657
4663 4673 4679 4691 4703 4721 4723 4729 4733 4751
4759 4783 4787 4789 4793 4799 4801 4813 4817 4831
4861 4871 4877 4889 4903 4909 4919 4931 4933 4937
4943 4951 4957 4967 4969 4973 4987 4993 4999 5003
5009 5011 5021 5023 5039 5051 5059 5077 5081 5087
5099 5101 5107 5113 5119 5147 5153 5167 5171 5179
5189 5197 5209 5227 5231 5233 5237 5261 5273 5279
5281 5297 5303 5309 5323 5333 5347 5351 5381 5387
5393 5399 5407 5413 5417 5419 5431 5437 5441 5443
5449 5471 5477 5479 5483 5501 5503 5507 5519 5521
5527 5531 5557 5563 5569 5573 5581 5591 5623 5639
5641 5647 5651 5653 5657 5659 5669 5683 5689 5693
5701 5711 5717 5737 5741 5743 5749 5779 5783 5791
5801 5807 5813 5821 5827 5839 5843 5849 5851 5857
5861 5867 5869 5879 5881 5897 5903 5923 5927 5939
5953 5981 5987 6007 6011 6029 6037 6043 6047 6053
6067 6073 6079 6089 6091 6101 6113 6121 6131 6133
6143 6151 6163 6173 6197 6199 6203 6211 6217 6221
6229 6247 6257 6263 6269 6271 6277 6287 6299 6301
6311 6317 6323 6329 6337 6343 6353 6359 6361 6367
6373 6379 6389 6397 6421 6427 6449 6451 6469 6473
6481 6491 6521 6529 6547 6551 6553 6563 6569 6571
6577 6581 6599 6607 6619 6637 6653 6659 6661 6673
6679 6689 6691 6701 6703 6709 6719 6733 6737 6761
6763 6779 6781 6791 6793 6803 6823 6827 6829 6833
6841 6857 6863 6869 6871 6883 6899 6907 6911 6917
6947 6949 6959 6961 6967 6971 6977 6983 6991 6997
7001 7013 7019 7027 7039 7043 7057 7069 7079 7103
7109 7121 7127 7129 7151 7159 7177 7187 7193 7207
7211 7213 7219 7229 7237 7243 7247 7253 7283 7297
7307 7309 7321 7331 7333 7349 7351 7369 7393 7411
7417 7433 7451 7457 7459 7477 7481 7487 7489 7499
7507 7517 7523 7529 7537 7541 7547 7549 7559 7561
7573 7577 7583 7589 7591 7603 7607 7621 7639 7643
7649 7669 7673 7681 7687 7691 7699 7703 7717 7723
7727 7741 7753 7757 7759 7789 7793 7817 7823 7829
7841 7853 7867 7873 7877 7879 7883 7901 7907 7919
Пов'язані сторінки
- Відмінний прайм Jens Kruse Andersen в арифметичних записах прогресії
 Список літератури
Список літератури
- BH77
- К. Байес і Р. Хадсон , "сегментований сит Ератосфена та простих чисел в арифметичній прогресії", Нордіск Тідскр. Інформація прозабезпечення (BIT) , 17 : 2 (1977) 121-127. ЗМ 56: 5405
- Чолова44
- С. Чаула , "Існує нескінченність 3 - комбінацій простих чисел у ПП", Проц. Лахор Філ. Соц. , 6 (1944) 15--16. ЗМ 7,243 л
- Corput1939
- А. Г. ван дер Кортут , "Супермен від Примзаглан і Примзалккатраен", Математика. Енн , 116 (1939) 1--50.
- DN97
- Х. Дубнер та Н. Нельсон , "Сім послідовних простих чисел в арифметичній прогресії", Матем. Комп. , 66 (1997) 1743-1749. ЗМ 98а: 11122 ( Реферат доступний )
- GH79
- Е. Гросвальд і П. Хагіс- молодший , "Арифметична прогресія, що складається лише з простих чисел", Математика. Комп. , 33 : 148 (жовтень 1979 р.) 1343-1352 рр. MR 80k: 10054 ( Реферат доступний )
- Гросвальд82
- Е. Гросвальд , "Арифметичні прогресії, які складаються тільки з простих чисел", J. Теорія чисел , 14(1982) 9--31. MR 83k: 10081
- GT2004a
- Грін, Бен і Дао, Теренс , "Прості містять довільно довгі арифметичні прогресії," Ann. математики. (2) , 167 : 2 (2008) 481-547. ( http://dx.doi.org/10.4007/annals.2008.167.481 ) MR 2415379
- GT2004b
- Б. Грін і Т. Тао , "Межа для прогресії довжини k в простих числах" (2004) Доступно з http://people.maths.ox.ac.uk/greenbj/papers/back-of-an- конверт.pdf .
- GT2006a
- Грін, Бенджамін і Дао, Теренс , "Лінійні рівняння в простих", Ann. математики. (2) , 171 : 3 (2010) 1753--1850. ( http://dx.doi.org/10.4007/annals.2010.171.1753 ) MR 2680398
- Гай94 (розділ A6)
- Р. К. Гай , Нерозв'язані проблеми теорії чисел , Springer-Verlag, 1994. Нью-Йорк, штат Нью-Йорк, ISBN 0-387-94289-0. MR 96e: 11002 [Відмінний ресурс! Гай коротко описує безліч відкритих питань, а потім надає численні посилання. Переглянути нові версії цього тексту.]
- LP67
- Л. Я. Лендер та Т. Р. Паркін , "Про перший появі первинних відмінностей", Математика. Комп. , 21 : 99 (1967) 483-488. MR 37: 6237
- Rose94 (Chп.13)
- А. Е. Роуз , курс з теорії чисел , друге видання, Clarendon Press, 1994. Нью-Йорк, с. Xvi + 398, ISBN 0-19-853479-5; 0-19-852376-9. MR 96g: 11001 ( Анотація доступна )
Арифметична прогресія простих чисел є безліччю простих чисел виду 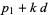 для фіксованого
для фіксованого 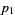 та
та 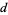 й послідовних
й послідовних 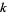 , тобто
, тобто 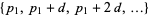 . Наприклад, 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 є 10-терміновою арифметичною прогресією простих чисел з різницею 210.
. Наприклад, 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 є 10-терміновою арифметичною прогресією простих чисел з різницею 210.
Давно доведено, що існують довільно довгі послідовності простих чисел в арифметичній прогресії (Guy 1994). Ще в 1770 році Лагранж і Варинг досліджували, наскільки велика загальна різниця арифметичної прогресії 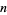 простих чисел. У 1923 році Харді та Літлвуд (1923) зробили дуже загальну гіпотезу, відому як гіпотеза k- tuple про розподіл первинних сузір'їв, що включає в себе гіпотезу, що існує нескінченно довгий простий арифметичний прогрес, як особливий випадок. Згодом важливий додатковий теоретичний прогрес зробив ван дер Кортут (1939), який довів, що в арифметичній прогресії існує нескінченно багато трійок простих чисел, а Хіт-Браун (1981), які довели, що існує нескінченно багато чотирирічного прогресії, що складаються з три прості числа і число, яке є або первинним, або напівпринципом .
простих чисел. У 1923 році Харді та Літлвуд (1923) зробили дуже загальну гіпотезу, відому як гіпотеза k- tuple про розподіл первинних сузір'їв, що включає в себе гіпотезу, що існує нескінченно довгий простий арифметичний прогрес, як особливий випадок. Згодом важливий додатковий теоретичний прогрес зробив ван дер Кортут (1939), який довів, що в арифметичній прогресії існує нескінченно багато трійок простих чисел, а Хіт-Браун (1981), які довели, що існує нескінченно багато чотирирічного прогресії, що складаються з три прості числа і число, яке є або первинним, або напівпринципом .
Проте, незважаючи на всі ці роботи, доказ загального результату для довільно довгих послідовностей простих чисел залишається відкритою гіпотезою (Гай 1994, стор. 15). Завдяки новій роботі Бена Гріна та Теренса Тао, здається, що припущення остаточно вирішено в позитивному. У нещодавно опублікованій препринті Грін та Тао (2004) використовують важливий результат, відомий як теорема Семереді в поєднанні з недавніми роботами Гольдстона та Йілдіріма, розумним "принципом переносу" та 48 сторінками щільної та технічної математики, що, очевидно, встановлюють основна теорема про те, що простими числами містяться арифметичні прогресії довжини 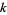 для всіх
для всіх 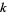 (Weisstein 2004). Однак доказ неконструктивний .
(Weisstein 2004). Однак доказ неконструктивний .
Дозвольте 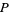 бути зростаючою арифметичною прогресією
бути зростаючою арифметичною прогресією 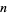 простих чисел з мінімальною різницею
простих чисел з мінімальною різницею 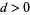 . Якщо простий
. Якщо простий 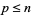 не ділиться
не ділиться 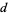 , то елементи
, то елементи 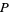 повинні мати всі залишки по модулю
повинні мати всі залишки по модулю 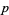 , зокрема, який-небудь елемент
, зокрема, який-небудь елемент 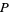 повинен бути делимий на
повинен бути делимий на 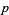 . Оскільки
. Оскільки 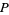 містить лише прості числа, цей елемент повинен бути рівним
містить лише прості числа, цей елемент повинен бути рівним 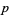 .
.
(1)
|
Нехай 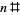 позначимо первородство з
позначимо первородство з 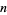 . Тоді , якщо
. Тоді , якщо 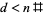 деякий прем'єр
деякий прем'єр 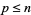 не поділяє
не поділяє 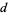 , і що прем'єр
, і що прем'єр 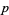 в
в 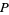 . Таким чином, для того, щоб визначити, чи
. Таким чином, для того, щоб визначити, чи 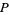 має
має 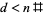 він, потрібно лише перевірити кінцеве число можливих
він, потрібно лише перевірити кінцеве число можливих 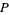 (тих,
(тих, 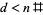 що містять і містять прості
що містять і містять прості 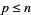 ), щоб побачити, чи вони містять лише прості числа. Якщо ні, тоді
), щоб побачити, чи вони містять лише прості числа. Якщо ні, тоді 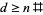 . Якщо
. Якщо 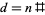 , тоді елементи
, тоді елементи 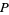 не можуть бути зроблені для покриття всіх залишків будь-якого простого
не можуть бути зроблені для покриття всіх залишків будь-якого простого 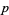 . В K -кратної гіпотеза потім стверджує , що існує безліч арифметичних прогресій простих чисел з різницею
. В K -кратної гіпотеза потім стверджує , що існує безліч арифметичних прогресій простих чисел з різницею 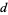 .
.
Обчислення показують, що найменша можлива загальна різниця для набору 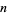 або більше простих чисел в арифметичній прогресії для
або більше простих чисел в арифметичній прогресії для 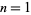 2, 3, ... становить 0, 1, 2, 6, 6, 30, 150, 210, 210, 210, 2310 , 2310, 30030, 30030, 30030, 30030, 510510, ... (OEIS A033188 , Ribenboim 1989, Dubner and Nelson 1997). Значення дорівнює
2, 3, ... становить 0, 1, 2, 6, 6, 30, 150, 210, 210, 210, 2310 , 2310, 30030, 30030, 30030, 30030, 510510, ... (OEIS A033188 , Ribenboim 1989, Dubner and Nelson 1997). Значення дорівнює 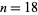 строгим, а решту - нижніми межами, які вважатимуть справедливістю гіпотези k- tuple і просто даються
строгим, а решту - нижніми межами, які вважатимуть справедливістю гіпотези k- tuple і просто даються 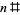 . Найменшими першими умовами арифметичної прогресії
. Найменшими першими умовами арифметичної прогресії 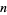 простих чисел з мінімальними відмінностями є 2, 2, 3, 5, 5, 7, 7, 199, 199, 199, 60858179, 147692845283, 14933623, 834172298383, ... (OEIS A033189; Вілсон).
простих чисел з мінімальними відмінностями є 2, 2, 3, 5, 5, 7, 7, 199, 199, 199, 60858179, 147692845283, 14933623, 834172298383, ... (OEIS A033189; Вілсон).
Менші перші терміни можливі для немінімальних термінових 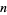 прогресів. Приклади включають 8-терміновий прогрес
прогресів. Приклади включають 8-терміновий прогрес 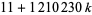 для
для 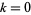 1, ..., 7, 12-терміни прогресування
1, ..., 7, 12-терміни прогресування 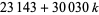 для
для 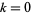 , 1, ..., 11 (Голубєв 1969, Гай 1994), а також 13-термін арифметичної прогресії
, 1, ..., 11 (Голубєв 1969, Гай 1994), а також 13-термін арифметичної прогресії 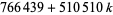 для
для 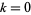 1, ..., 12 (Гай 1994).
1, ..., 12 (Гай 1994).
Наступна таблиця підсумовує найбільшу відомі арифметичні прогресії 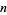 простих чисел для малих
простих чисел для малих 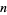 , де
, де
(2)
|
| прості числа для | цифри | довідка | |
| 3 | 137514 | J. K. Anderson et al. (2007) | |
| 4 | 11961 | К. Девіс (2008) | |
| 5 | 6913 | Д. Бродхерст (2008) | |
| 6 | 1606 р | К. Девіс (2006) | |
| 7 | 1290 | К. Девіс (2006) | |
| 8 | 1037 | П. Андервуд (2003) | |
| 9 | 401 | М. Оукс (2006) |
Більш повний стіл підтримує Андерсен.
(3)
|
для 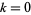 , 1, ..., 5 (Лендер і Паркін, 1967, Дубнер і Нельсон, 1997).
, 1, ..., 5 (Лендер і Паркін, 1967, Дубнер і Нельсон, 1997).
Найбільший відомий випадок трьох послідовних простих чисел в арифметичній прогресії є 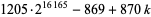 для
для 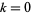 , 1, 2, знайдена Т. Альм, Х. Rosenthal, J. K. Andersen, Р. Ballinger в 2003.
, 1, 2, знайдена Т. Альм, Х. Rosenthal, J. K. Andersen, Р. Ballinger в 2003.
Найбільша відома послідовність послідовних простих чисел в арифметичній прогресії (тобто всі числа між першим і останнім членами у прогресії, крім самих членів, є складовими) становить десять, заданих
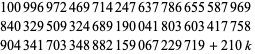 |
(4)
|
для 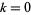 , 1, ..., 9 (OEIS A033290 ), виявлені Гарві Дубнером, Тоні Форбсом, Манфредом Топліком та ін. 2 березня 1998 р. За словами Дубнера та співавт., перед тим як шукати послідовність з 11 послідовних простих чисел , потрібна трильйонкратне збільшення швидкості комп'ютера, тому вони очікують, що запис десятизначного числа триватиме довго приходити.
, 1, ..., 9 (OEIS A033290 ), виявлені Гарві Дубнером, Тоні Форбсом, Манфредом Топліком та ін. 2 березня 1998 р. За словами Дубнера та співавт., перед тим як шукати послідовність з 11 послідовних простих чисел , потрібна трильйонкратне збільшення швидкості комп'ютера, тому вони очікують, що запис десятизначного числа триватиме довго приходити.
Це побиває запис дев'яти простих рядів, встановлених 15 січня 1998 тими самими слідчими
 |
(5)
|
для 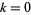 , 1, ..., 8 (тепер відомі дві послідовності з дев'яти), прогресування восьми послідовних простих чисел, заданих
, 1, ..., 8 (тепер відомі дві послідовності з дев'яти), прогресування восьми послідовних простих чисел, заданих
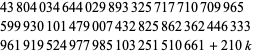 |
(6)
|
для 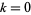 , 1, ..., 7, виявлені Гарві Дубнер, Тоні Форбс та ін. 7 листопада 1997 р. (нині відомо декілька), а прогрес семи дано
, 1, ..., 7, виявлені Гарві Дубнер, Тоні Форбс та ін. 7 листопада 1997 р. (нині відомо декілька), а прогрес семи дано
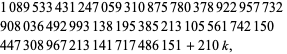 |
(7)
|
для 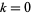 , 1, ..., 6, відкритий Г. Дубнер та Г. К. Нельсон 29 серпня 1995 р. (Peterson 1995, Dubner and Nelson, 1997).
, 1, ..., 6, відкритий Г. Дубнер та Г. К. Нельсон 29 серпня 1995 р. (Peterson 1995, Dubner and Nelson, 1997).
Циммерманн, П. http://www.loria.fr/~zimmerma/records/8primes.announce . 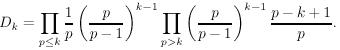
Немає коментарів:
Дописати коментар