Розглянемо рівняння
на множині дійсних чисел:
де z – довільне дійсне додатне або від’ємне число,
тобто дана пара задовольняє дане рівняння.
тоді можна розглядати
пару:
що задовольняє дане рівняння.
дана пара задовольняє дане
рівняння,
дана пара задовольняє дане
рівняння.
дана пара задовольняє дане
рівняння.
дана пара задовольняє дане
рівняння.
де z – довільне дійсне додатне або від’ємне число,
тобто дана пара задовольняє дане рівняння.
тоді можна розглядати пару:
що задовольняє дане рівняння.
дана пара задовольняє дане рівняння,
дана пара задовольняє дане рівняння.
дана пара задовольняє дане рівняння.
дана пара задовольняє дане рівняння.
Ламбертa W-Функція
(1)
|
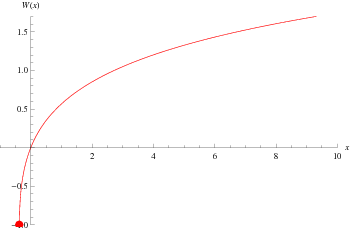
Графік вище показує функцію уздовж реальної осі . Основне значення функції Ламберта 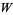 реалізовано в мові Вольфрам як ProductLog [ z ]. Різні гілки функції доступні в мові Вольфрам як ProductLog [ k , z ], де
реалізовано в мові Вольфрам як ProductLog [ z ]. Різні гілки функції доступні в мові Вольфрам як ProductLog [ k , z ], де 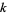 є будь-яке ціле число і
є будь-яке ціле число і 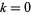 відповідає основному значенню. Незважаючи на відсутність документів, LambertW [ k , z ] автоматично оцінює ProductLog [ k , z ] у мові Вольфрам.
відповідає основному значенню. Незважаючи на відсутність документів, LambertW [ k , z ] автоматично оцінює ProductLog [ k , z ] у мові Вольфрам.
Ламберт (1758) розглянув рішення
(2)
|
тепер відомий як трансцендентне рівняння Ламберта . Ейлер почув про папір Ламберта в 1764 році, коли Ламберт переїхав з Цюріха до Берліна. Після деяких приватних суперечок про пріоритети деяких родинних розширень серії в 1770/1771 р. Ейлер (1783) написав статтю про трансцендентне рівняння Ламберта, в якій він ввів особливий випадок, який зводиться до 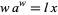 , що є майже визначенням
, що є майже визначенням 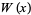 , хоча Ейлер запропонував визначити функція більше схожа на
, хоча Ейлер запропонував визначити функція більше схожа на 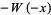 . У цьому документі Ейлер розглядав ряд рішень, а в першому параграфі явно цитує Ламберта як того, хто вперше розглянув це рівняння.
. У цьому документі Ейлер розглядав ряд рішень, а в першому параграфі явно цитує Ламберта як того, хто вперше розглянув це рівняння.
Ейзенштейн (1844) розглянув серію нескінченної енергетичної вежі
(3)
|
який може бути виражений у замкнутому вигляді як
(4)
|
Pólya і Szegö (1925) першими використовували символ 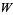 функції Ламберта.
функції Ламберта.
Банел і Джейакумар (2000) показали, що a 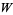 -функція описує співвідношення між напругою, струмом та опором в діоді, а Пакель та Юен (2004) застосували
-функція описує співвідношення між напругою, струмом та опором в діоді, а Пакель та Юен (2004) застосували  -функцію до балістичного снаряда за наявності опору повітря. Інші застосунки були знайдені в статистичній механіці, квантовій хімії, комбінаториці, кінетиці ферментів, фізіології зору, інженерії тонких плівок, гідрології та аналізу алгоритмів (Hayes 2005).
-функцію до балістичного снаряда за наявності опору повітря. Інші застосунки були знайдені в статистичній механіці, квантовій хімії, комбінаториці, кінетиці ферментів, фізіології зору, інженерії тонких плівок, гідрології та аналізу алгоритмів (Hayes 2005).
 |
Функція Ламберта  показана вище на складній площині.
показана вище на складній площині.

Речові (ліві) і уявні (правильні) частини аналітичного продовження 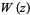 над комплексною площиною наведені вище (М. Тротт, пер. Комм.).
над комплексною площиною наведені вище (М. Тротт, пер. Комм.).
(5)
| |||
(6)
| |||
(7)
| |||
(8)
|
(9)
|
давати
(10)
|
Функція Ламберта  підпорядковується ідентичності
підпорядковується ідентичності
(11)
|
(персонал від Р. Корлеса до О. Марічева, 29 вересня 2015 р.).
 |
Функція 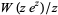 має дуже складну структуру в комплексній площині, але просто дорівнює 1 для
має дуже складну структуру в комплексній площині, але просто дорівнює 1 для ![R [z]> = 1](http://mathworld.wolfram.com/images/equations/LambertW-Function/Inline30.gif) і трохи розширеної області вище і нижче реальної осі.
і трохи розширеної області вище і нижче реальної осі.
Функція Ламберта 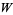 має розширення ряду
має розширення ряду
(12)
| |||
(13)
|
(14)
|
де 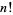 це факторіала . Однак ця серія коливається між все більшими позитивними та негативними значеннями для реальних
це факторіала . Однак ця серія коливається між все більшими позитивними та негативними значеннями для реальних 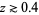 , і тому не може бути використана для практичного чисельного обчислення.
, і тому не може бути використана для практичного чисельного обчислення.
(15)
| |||
![(L_2) (L_2) (L_2) (L_2) / (L_1) + (L_2 (-2 + L_2)) / (2L_1 ^ 2) + (L_2 (6-9L_2 + 2L_2 ^ 2)) / (6L_1 ^ 3) + (L_2 (- 12 + 36L_2-22L_2 ^ 2 + 3L_2 ^ 3)) / (12L_1 ^ 4) + (L_2 (60-300L_2 + 350L_2 ^ 2-125L_2 ^ 3 + 12L_2 ^ 4)) / (60L_1 ^ 5) + O [ (L_2) / (L_1)) ^ 6],](http://mathworld.wolfram.com/images/equations/LambertW-Function/Inline46.gif) |
(16)
|
де
(17)
| |||
(18)
|
(Corless et al., 1996), виправлення друкарської помилки в Брюїні (1981). Інша експансія завдяки Госперу (пер. Кому., 22 липня 1996 р.) Є подвійною серією
![W (x) = a + sum_ (n = 0) ^ infty {sum_ (k = 0) ^ n (S_1 (n, k)) / [[ln (x / a) -a] ^ (k-1) (n-k + 1)!)) [1- (ln (x / a)) / a] ^ n,](http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation9.gif) |
(19)
|
де 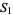 є неотрицательным номером Стірлінга першого роду і
є неотрицательным номером Стірлінга першого роду і 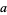 є першим наближенням, яке можна використовувати для вибору між гілками. Функція Ламберта
є першим наближенням, яке можна використовувати для вибору між гілками. Функція Ламберта 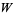 є двозначною для
є двозначною для 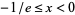 . Для
. Для 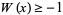 , функція позначена
, функція позначена 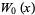 або просто
або просто 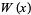 , і це називається головною гілкою . Для
, і це називається головною гілкою . Для 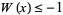 цього позначається функція
цього позначається функція 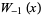 . Похідною від
. Похідною від 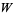 IS
IS
(20)
| |||
(21)
|
(22)
|
Тоді 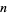 похідні Ламберта
похідні Ламберта 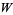 -функції задані
-функції задані
(23)
|
де 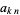 номер трикутник
номер трикутник
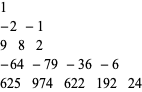 |
(24)
|
(25)
| |||
(26)
|
Немає коментарів:
Дописати коментар